Modelling the brain as a poroelastic medium

At the organ-level and at the time scale of seconds to weeks, the brain can be viewed as a poroelastic medium. Brain tissue is soft and elastic, and permeated by a number of networks filled with water-like fluids - including blood vessels filled with blood, cellular networks filled with intracellular fluid, and interstitial space in between the cells filled with interstitial fluid. Moreover, the living brain is never still: the brain and its surroundings pulsate in rhythm with the heart beat and with respiration in an intricate mechanical, chemical and electrical interplay.  These physiological processes are essential for the well-being of the brain, but many aspects remain poorly understood. For instance, the mechanical and chemical interplay in the brain and its environment is hypothesized to be crucial for neurological disorders such as e.g. normal pressure hydrocephalus, and for neurodegenerative disorders such as e.g. Alzheimer’s disease. Mathematical modelling and computer simulations are emerging as powerful avenues of investigation to complement to experimental and clinical techniques.  The poroelastic brain can be modelled via Biot’s equations or more generally via multiple-network poroelasticity theory (MPET). These homogenized, time-dependent systems of partial differential equations are based on first principles (balance of momentum and balance of mass) and can describe the displacement, solid stress and fluid pressures of the brain and its fluid networks in time and space subject to external forces.  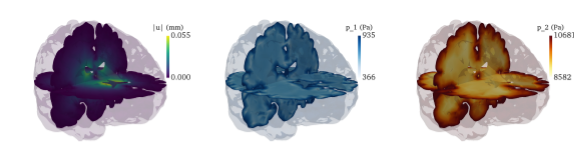Figure: (From left to right): Snapshots of (i) simulated displacement magnitude, homogenized pressure in (ii) the interstitial fluid and (iii) arterial blood at peak arterial inflow computed using the MPET equations subject to external pulsations, see [Lee, Jeonghun J., et al. (2019)].